Momen inersia

بِسْــــــــــــــــمِ اﷲِالرَّحْمَنِ الرَّحِيم

Momen inersia (Satuan SI : kg m²)adalah ukuran kelembaman suatu benda untuk berotasi terhadap porosnya. Besaran ini adalah analog rotasi daripada massa. Momen inersia berperan dalam dinamika rotasi seperti massa dalam dinamika dasar, dan menentukan hubungan antara momentum sudut dan kecepatan sudut, momen gaya dan percepatan sudut, dan beberapa besaran lain. Meskipun pembahasan skalar terhadap momen inersia, pembahasan menggunakan pendekatan tensor memungkinkan analisis sistem yang lebih rumit seperti gerakan giroskopik.

Lambang I dan kadang-kadang juga J biasanya digunakan untuk merujuk kepada momen inersia.

Definisi sederhana momen inersia (terhadap sumbu rotasi tertentu) dari sembarang objek, baik massa titik atau struktur tiga dimensi, diberikan oleh rumus:

$I = \int r^2 \,dm\,\!$

di mana m adalah massa dan r adalah jarak tegak lurus terhadap sumbu rotasi.

Analisis

Momen inersia (skalar) sebuah massa titik yang berputar pada sumbu yang diketahui didefinisikan oleh

$I \triangleq m r^2\,\!$

Momen inersia adalah aditif. Jadi, untuk sebuah benda tegar yang terdiri atas N massa titik m_i dengan jarak r_i terhadap sumbu rotasi, momen inersia total sama dengan jumlah momen inersia semua massa titik:

$I \triangleq \sum_{i=1}^{N} {m_{i} r_{i}^2}\,\!$

Untuk benda pejal yang dideskripsikan oleh fungsi kerapatan massa ρ(r), momen inersia terhadap sumbu tertentu dapat dihitung dengan mengintegralkan kuadrat jarak terhadap sumbu rotasi, dikalikan dengan kerapatan massa pada suatu titik di benda tersebut:

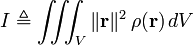
$I \triangleq \iiint_V \|\mathbf{r}\|^2 \,\rho(\mathbf{r})\,dV \!$